Peregrine falcons maneuver best when dive-bombing at more than 300 kilometers per hour (very interesting & with a video because, you know, math!)
http://www.sciencemag.org/news/2018/04/peregrine-falcons-maneuver-best-when-dive-bombing-more-300-kilometers-hour?utm_campaign=news_daily_2018-04-12&et_rid=213094054&et_cid=1969675Paper: Physics-based simulations of aerial attacks by peregrine falcons reveal that stooping at high speed maximizes catch success against agile prey
http://journals.plos.org/ploscompbiol/article?id=10.1371/journal.pcbi.1006044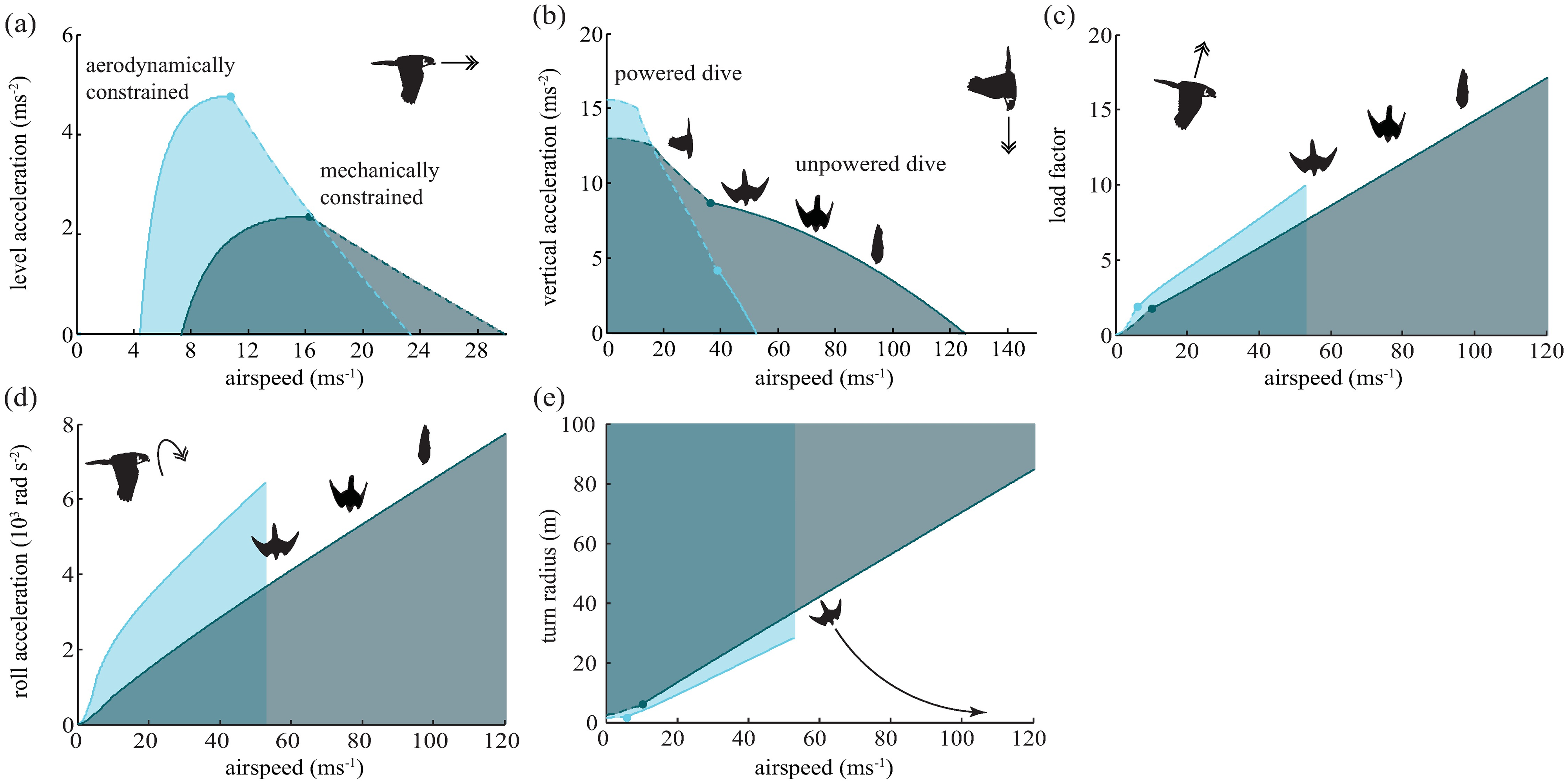
Flight performance graphs in the flight simulator for the peregrine falcon (dark blue) and the common starling (light blue).
The double arrows denote the direction of acceleration displayed in the graph. The starling is able to outmaneuver the falcon at a given airspeed, if there exists a region under the curve of the starling that is not overlapping with that of the falcon. (a) Level acceleration versus air speed: level flight with the requirement that lift equals weight. Dashed lines denote the speed wherein torque forces constrain the maximum acceleration (mechanical constraints). Top level flight speed is reached at the point where level acceleration is zero. (b) Vertical dive acceleration (including gravity) versus air speed. At the end of the dashed lines, flapping is substituted by gliding with retracted wings in order to maximize vertical acceleration. (c) Load factor versus air speed. The load factor is defined as lift divided by weight. The maximum load factor does not scale quadratically with forward speed due to constraints in torque forces [11]. Instead, wings are retracted optimally to increase maximum load. (d) Roll acceleration versus air speed. Roll acceleration determines the speed with which the bird can redirect its lift and is calculated by estimating the whole-body inertia around the roll-axis and the maximum net torque production [11]. (e) Turning radius is calculated as the square of air speed divided by the maximum normal acceleration.

 Author
Topic: New developments in the field of science (Read 759792 times)
Author
Topic: New developments in the field of science (Read 759792 times)
